The Ricci flow on the 2-sphere with marked points is shown to converge in all three stable semi-stable and unstable cases. It may well have been forgotten if it were not for Craig Hodgson still having a.

Hamilton S Ricci Flow Graduate Studies In Mathematics Bennett Chow Peng Lu And Lei Ni 9780821842317 Amazon Com Books
Remark 18 If we assume the existence of a lower bound for the functional E 1 E 0 then we are able.
. Rotational Solid 2D Uniformization Dimpled Sphere. Intuitively a surface Ricci flow is the process to. If one fails to do this the problem is that for example instead of evolving a given three-dimensional manifold into one of Thurstons canonical forms we might just shrink its size.
Understanding the singularities of the Ricci ow is not only an essential step in proving the geometrization of 3-manifolds but also of great signi cance in geometric anal-ysis. Conformal geometric maps have been used in. Three-sphere S3 or a quotient of S3 by a linear group of isometries.
Suppose S is a closed oriented surface 2-manifold embedded in R 3 which inherits the metric from R 3 so that distances are measured by shortest paths on the surface. RICCI FLOW ON KAHLER-EINSTEIN MANIFOLDS 19 Remark 17 We need the assumption on the existence of a Kahler-Einstein metric because we use a nonlinear inequality from 34. We conclude with a qualitative discussion of the ideas behind the proof of the Geometrization Conjecture using the Ricci ow.
Ricci flow is a powerful tool to compute surface uniformization deforming any arbitrary surfaces to one of the 3 canonical spaces with different background geometries the sphere the Euclidean plane or the hyperbolic disk. This paper originally written in the early eighties is published in the Collected Papers on Ricci Flow book edited by H-D. Most of the project is based on the book by Chow and Knopf 6 the notes by Peter Topping 28 which have recently been made into a book see 29 the papers of Richard Hamilton in particular 9 and the lecture.
We also give in dimension 3 a general contruction of Type I neckpinching and clarify the. I believe that the Ricci flow on orbifolds was first studied by Hamilton in the paper Three-Orbifolds with Positive Ricci Curvature answering a question of Thurston. The discrete computational algorithms can be found in 2629.
Anderson 184 NOTICESOFTHEAMS VOLUME51 NUMBER2 Introduction The classification of closed surfaces is a milestone in the development of topology so much so that it is now taught to most mathematics undergrad-uates as an introduction to topology. Two-dimensional topology All of the compact surfaces that anyone has ever seen. ˈ p w æ k ær eɪ US.
In this paper we propose a three-stage approach to manifold alignment using discrete surface Ricci flow. We construct examples of spherical space forms S3Γg with positive scalar curvature and containing no stable embedded minimal surfaces such that the following happens along the Ricci flow starting at S3Γg. CAO general 3-manifolds the Ricci ow could develop singularities.
Theorem 11 For any initial Sasakian structure on S3 of positive transverse scalar curvature the SasakiRicci flow converges exponentially to a gradient SasakiRicci soliton. Obtain persistent homological characterization of singularity formation in Ricci flow. Our main result is as follows.
3-sphere by nite groups of isometries acting freely. However on Partially supported by NSF grants DMS-0354621 and DMS-0506084. In mathematics the Poincaré conjecture UK.
A stable embedded minimal two-sphere appears and a non-trivial singularity occurs. Reversing the Ricci flow. Our approach transforms the original intrinsic manifolds to hyper spheres using conformal mapping in the first stage and then zooms these hyper spheres into the same scale and aligns them in the following stages.
Ricci Flow and the Sphere Theorem 51 pinched in the global sense must be homeomorphic to the standard sphere SnIn 1956 Milnor 8 had shown that there exist smooth manifolds which are homeo- morphic but not diffeomorphic to S7 so-called exotic 7-spheres. Introduction The classical uniformization theorem interpreted differential geomet-rically states that any Riemannian metric on a 2-dimensional surface is pointwise conformal to a constant curvature metric. In the stable case the flow was known to converge without any.
THE RICCI FLOW ON THE 2-SPHERE BENNETT CHOW 1. Of 3-Manifolds via the Ricci Flow Michael T. 12 Ricci Flow Recently the term of Ricci flow becomes popular due to the fact that it has been ap-plied for the proof of the Poincare conjecture on 3-manifolds 13.
The Ricci flow does not preserve volume so to be more careful in applying the Ricci flow to uniformization and geometrization one needs to normalize the Ricci flow to obtain a flow which preserves volume. ˌ p w æ k ɑː ˈ r eɪ French. Every simply connected closed 3-manifold is homeomorphic to the 3-sphere.
Pwɛkaʁe is a theorem about the characterization of the 3-sphere which is the hypersphere that bounds the unit ball in four-dimensional space. Ricci flow can also be generalized to compute general quasi-conformal maps by the auxiliary metric. Moreover we prove the.
We describe in details about our algorithm its theoretical principles our. Such an inequality is just the Moser-Trudinger-Onofri inequality if the underlying manifold is the Riemann sphere. A topological space is simply-connected if any closed curve in the space can be contin-uously.
PDF On Jan 1 1991 Bennett Chow published The Ricci flow on the 2-sphere Find read and cite all the research you need on ResearchGate. Since the so-lution of the uniformization problem for surfaces by Poincaré and Koebe this topological. Alsing Air Force Research Laboratory Rome NY.
Lectures on the ricci flow 1 Peter Topping March 9 2006 1 c Peter Topping 2004 2005 2006. Symmetric Dumbbell 3D Neckpinch Neckpinch. Ricci Flow on S2 and S3 Paul M.
RICCI FLOW AND THE SPHERE THEOREM KLAUSECKERBERLIN ThismonographgivesanaccountoftherecentproofofthefamousDifferentiable. How to distinguish the sphere from the other surfaces. Richard Hamilton introduced the Ricci flow for Riemannian manifolds of any dimension in his seminal work 4 in 1982.
An equivalent form of the. This shows that additional conditions have to be imposed in order for a manifold to be diffeomor-phic to. The SasakiRicci flow deforms Sasakian structures within a fixed class B.
The Ricci Flow Approach to 3-Manifold Topology John Lott. However many surface representations that use local shape signatures are not stable and cannot perform well in the presence of non-rigid deformation. The SasakiRicci Flow on Sasakian 3-Spheres 45 it is homologous to ηa.
The accuracy of the Ricci flow method for community detection on model networks. Shrinks to round point. If it is at least crudely accurate to say that Ricci flow smooths out the metriccurvature so that the surface eventually evolves to a sphere is.
These are all of the compact connected ori-ented surfaces without boundary. The accuracy is measured by the adjust Rand index ARI and each data point is. Discrete formulations useful for imaging Objective.
Thus one can con-sider the question of whether there is a natural evolution equation which conformally deforms any metric on a surface to a. 20 harmonic and conformal shape images 33 28 29 physics-based deformable models 26 Free-Form Deformation FFD 13 and Level-Set based meth-ods 17. Ricci Flow for 3D Shape Analysis.
Numerical Simulation Of Ricci Flow On A Era

Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar

Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar
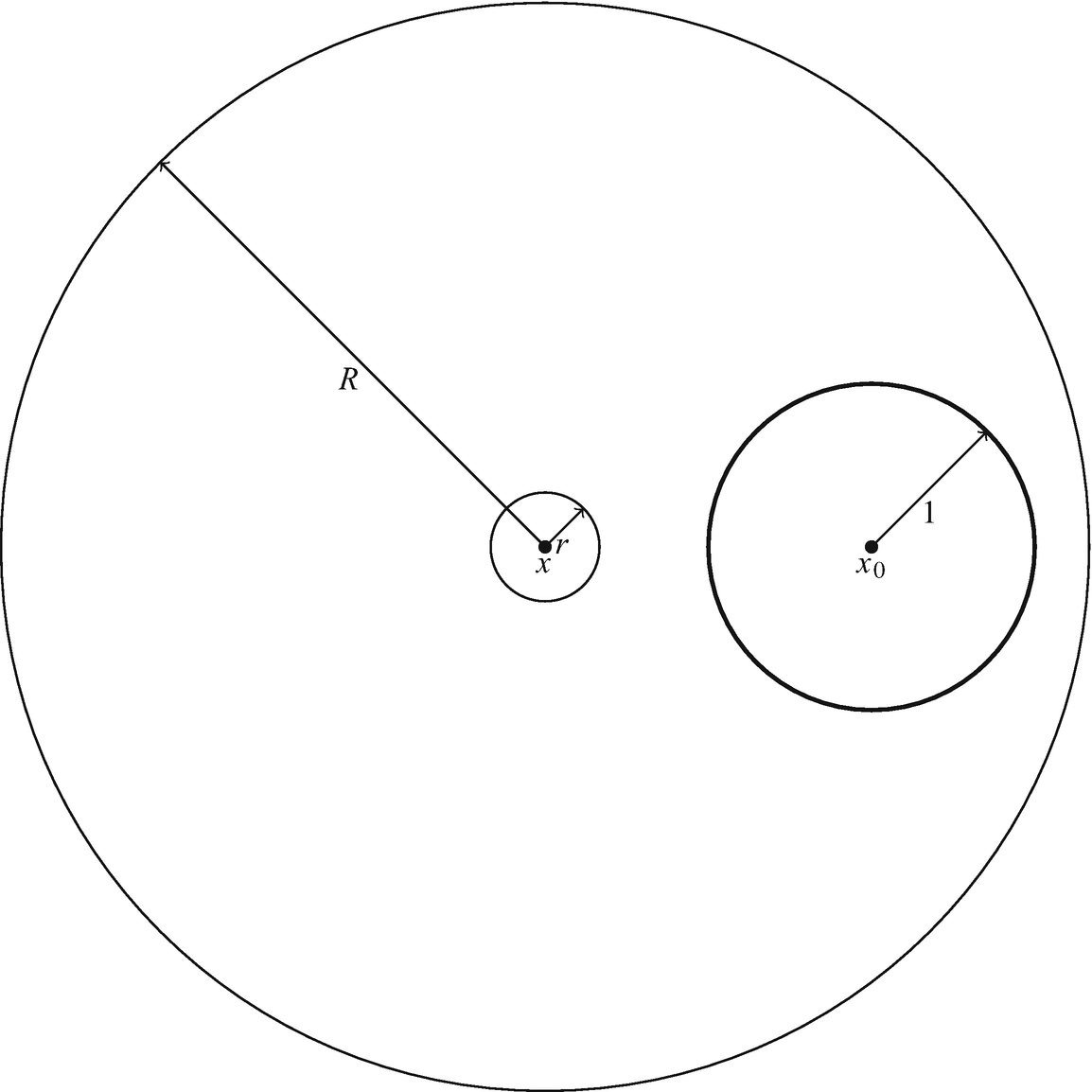
Ricci Flow And Ricci Limit Spaces Springerlink
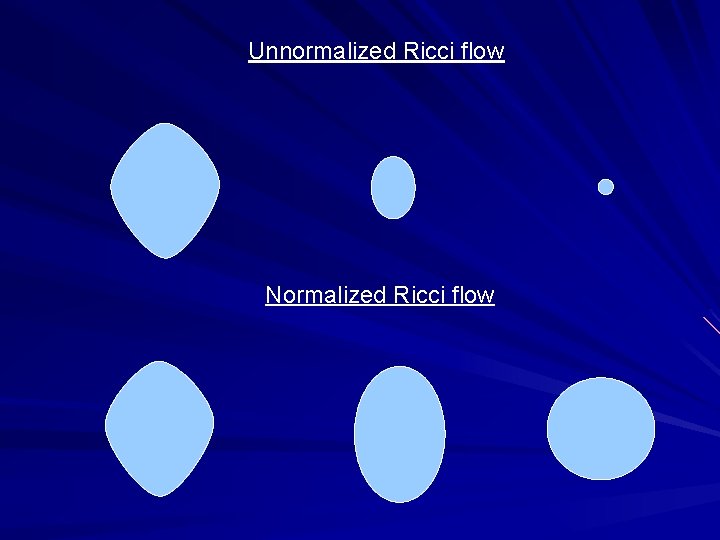
The Work Of Grigory Perelman Grigory Perelman Born
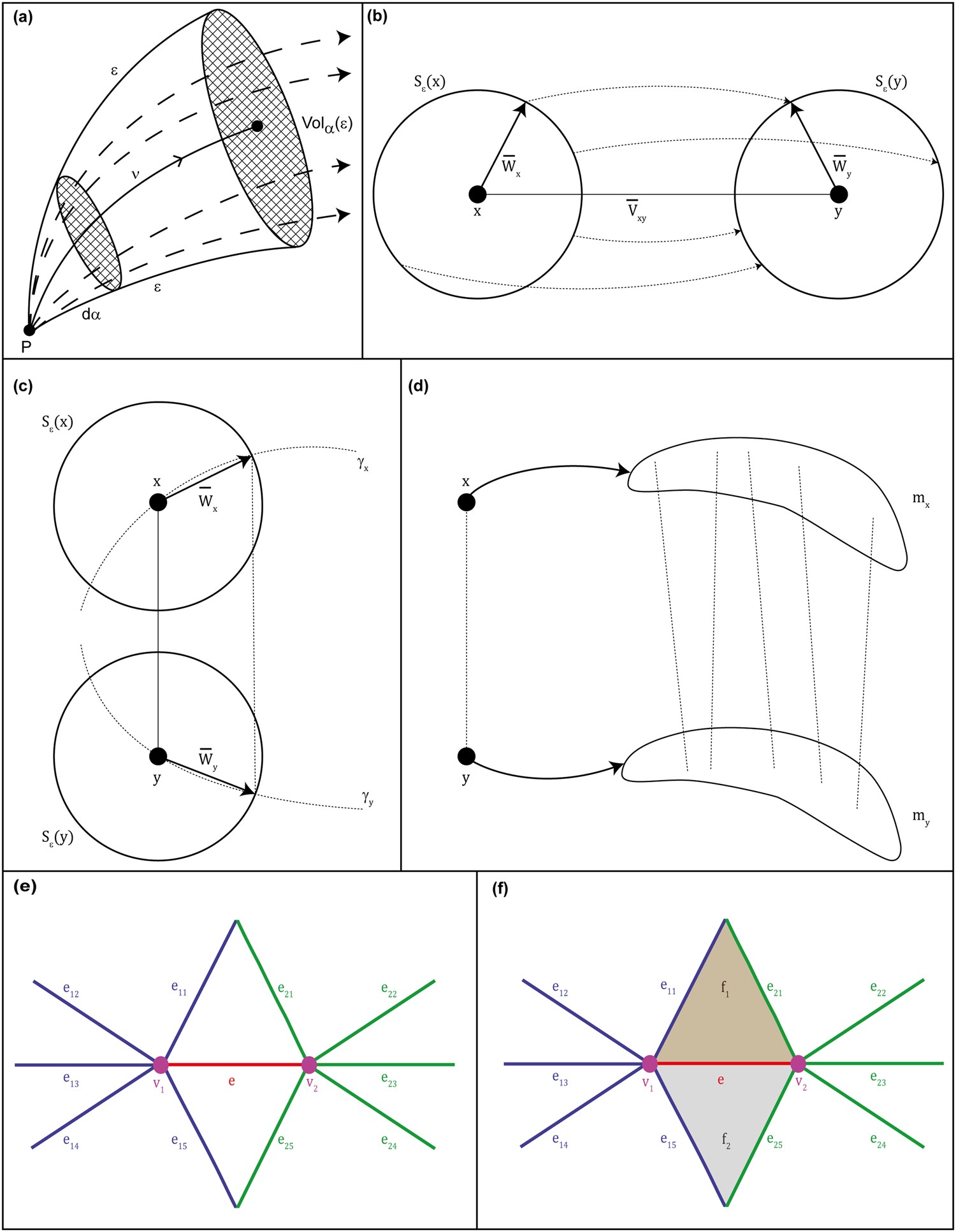
Comparative Analysis Of Two Discretizations Of Ricci Curvature For Complex Networks Scientific Reports

Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar

Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar
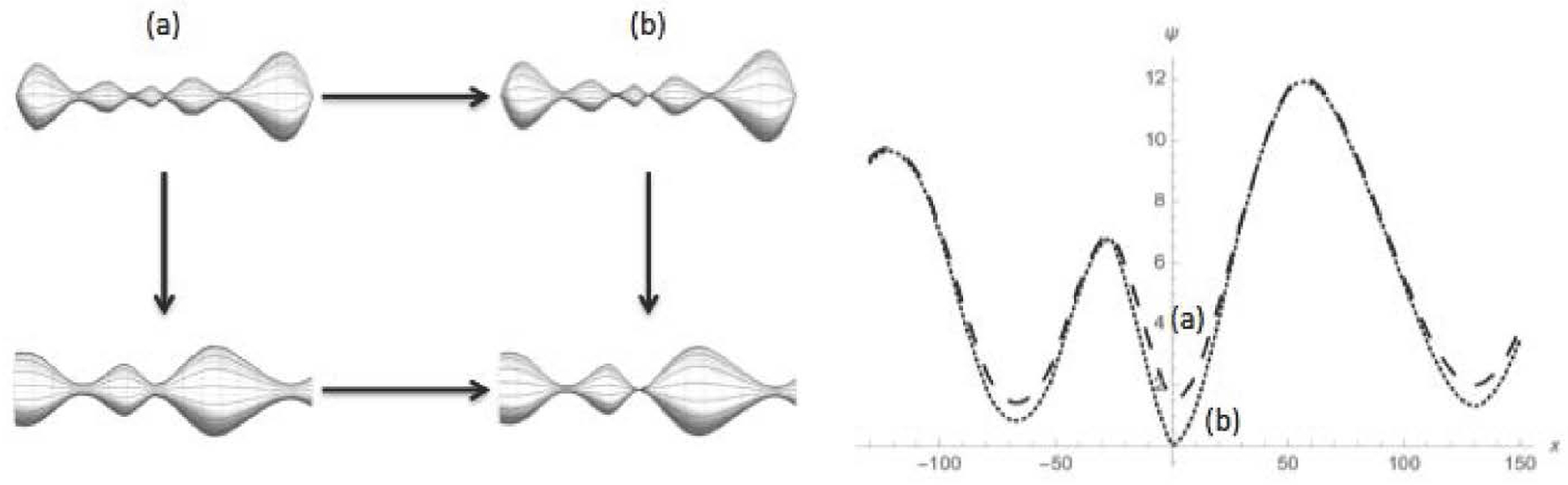
Axioms Free Full Text Topological Signals Of Singularities In Ricci Flow Html

Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar
Pdf The Ricci Flow In Riemannian Geometry A Complete Proof Of The Differentiable 1 4 Pinching Sphere Theorem Semantic Scholar

Perelman S Entropy Functionals And No Local Collapsing An Introduction To Perelman S First Paper Lakzian Sajjad 9783847372509 Amazon Com Books
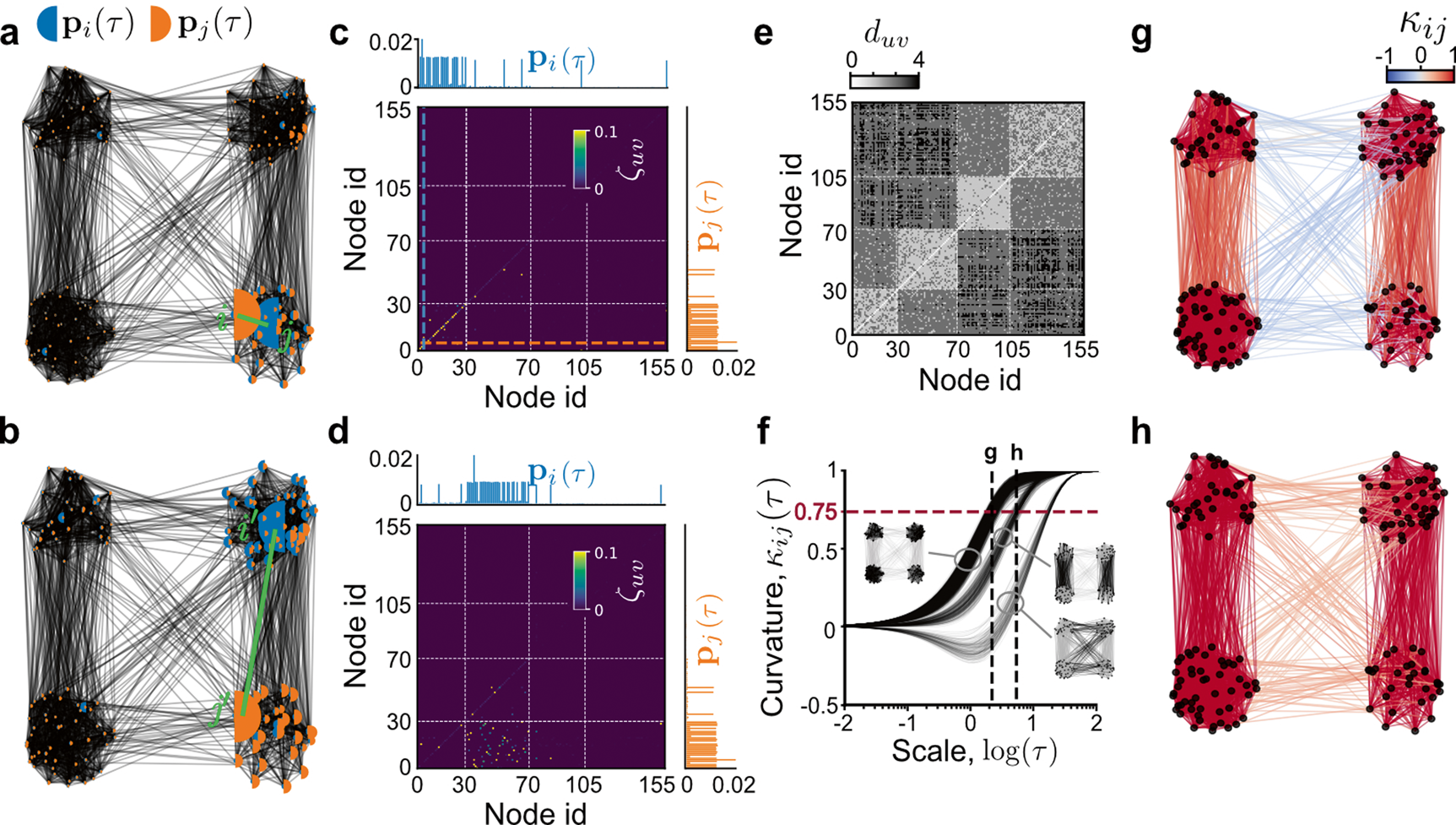
Unfolding The Multiscale Structure Of Networks With Dynamical Ollivier Ricci Curvature Nature Communications



0 komentar:
Posting Komentar